OEIS Sequences
- A230551 - \(\operatorname{Av}^I(2431)\)
- A230552 - \(\operatorname{Av}^I(2341)\)
- A230553 - \(\operatorname{Av}^I(1342)\)
- A001006 - \(\operatorname{Av}^I(1234)\)
- A230554 - \(\operatorname{Av}^I(1324)\)
- A230555 - \(\operatorname{Av}^I(3421)\)
- A230556 - \(\operatorname{Av}^I(4231)\)
- A121704 - \(\operatorname{Av}^I(2413)\)
Open Questions
- The enumerations (and, in particular, the exponential growth rates) of \(\operatorname{Av}^I(2431)\), \(\operatorname{Av}^I(1324)\), \(\operatorname{Av}^I(3421)\), and \(\operatorname{Av}^I(4231)\) are still unknown.
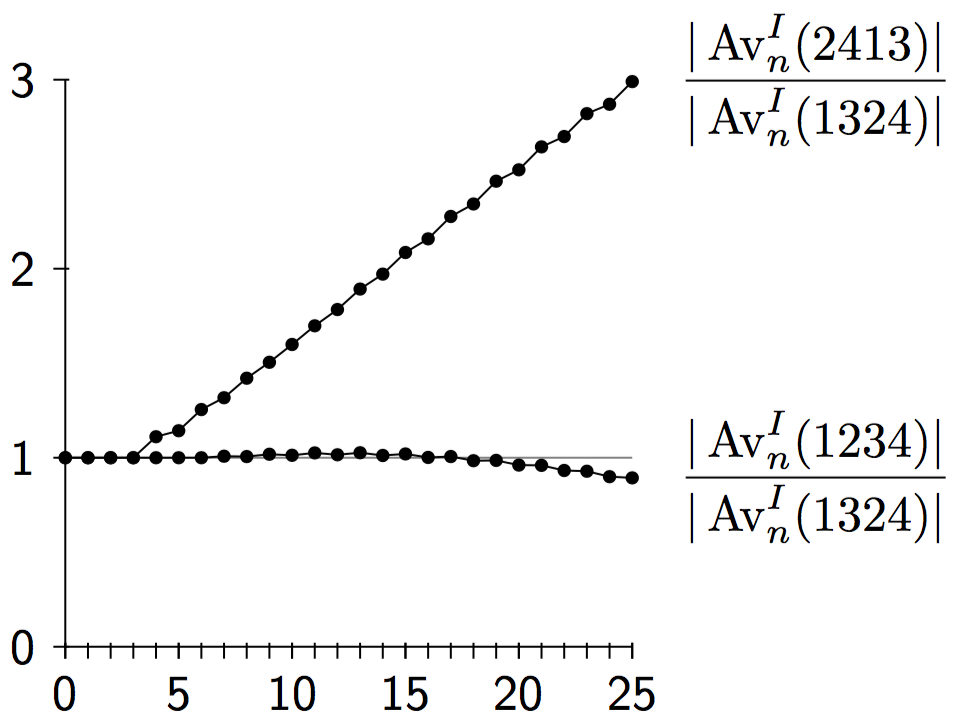
- The growth rate of the sequence \(|\text{Av}_n^I(2413)|\) is \(\approx 3.15\), while the growth rate of \(|\text{Av}_n^I(1324)|\) is known to be at least 3.13 and forthcoming results imply it is at least 3.20. Therefore, the ratios \(\displaystyle \frac{|\text{Av}_n^I(2413)|}{|\text{Av}_n^I(1324)|}\) eventually approach zero. However, as the chart below shows, the plot of the first 25 ratios is steadily increasing. When does the plot begin to decrease? When does it fall below 1? Understanding this may help understand the sequence \(|\text{Av}_n(1324)|\).