Areas of Research
My research can be broadly divided into three areas.
-
Devising algorithmic methods to automatically and rigorously discover and prove structural results for broad families of combinatorial sets.
My most significant work in this area is Combinatorial Exploration: An Algorithmic Framework for Enumeration and its accompanying website PermPAL (https://permpal.com). Several more papers extending this work are forthcoming, including an extension of the methods to the multivariate setting. -
Improving, implementing, and utilizing experimental methods to conjecture generating functions and asymptotic behavior of counting sequences.
These methods are used often throughout my other work, and I frequently receive requests from other researchers to apply them to counting sequences that they are investigating. See my software page for more information. - Investigating the enumeration and asymptotic behavior of particular combinatorial sets.
See, e.g.:
We prove that any class of permutations defined by avoiding a partially ordered pattern (POP) with height at most two has a regular insertion encoding and thus has a rational generating function. Then, we use Combinatorial Exploration to find combinatorial specifications and generating functions for hundreds of other permutation classes defined by avoiding a size 5 POP, allowing us to resolve several conjectures of Gao and Kitaev and of Chen and Lin.

The Enumeration of Inversion Sequences Avoiding the Patterns 201 and 210.
We derive the algebraic generating function for inversion sequences avoiding the patterns 201 and 210 by describing a set of succession rules, converting them to a system of generating function equations with one catalytic variable, and then solving the system with kernel method techniques.
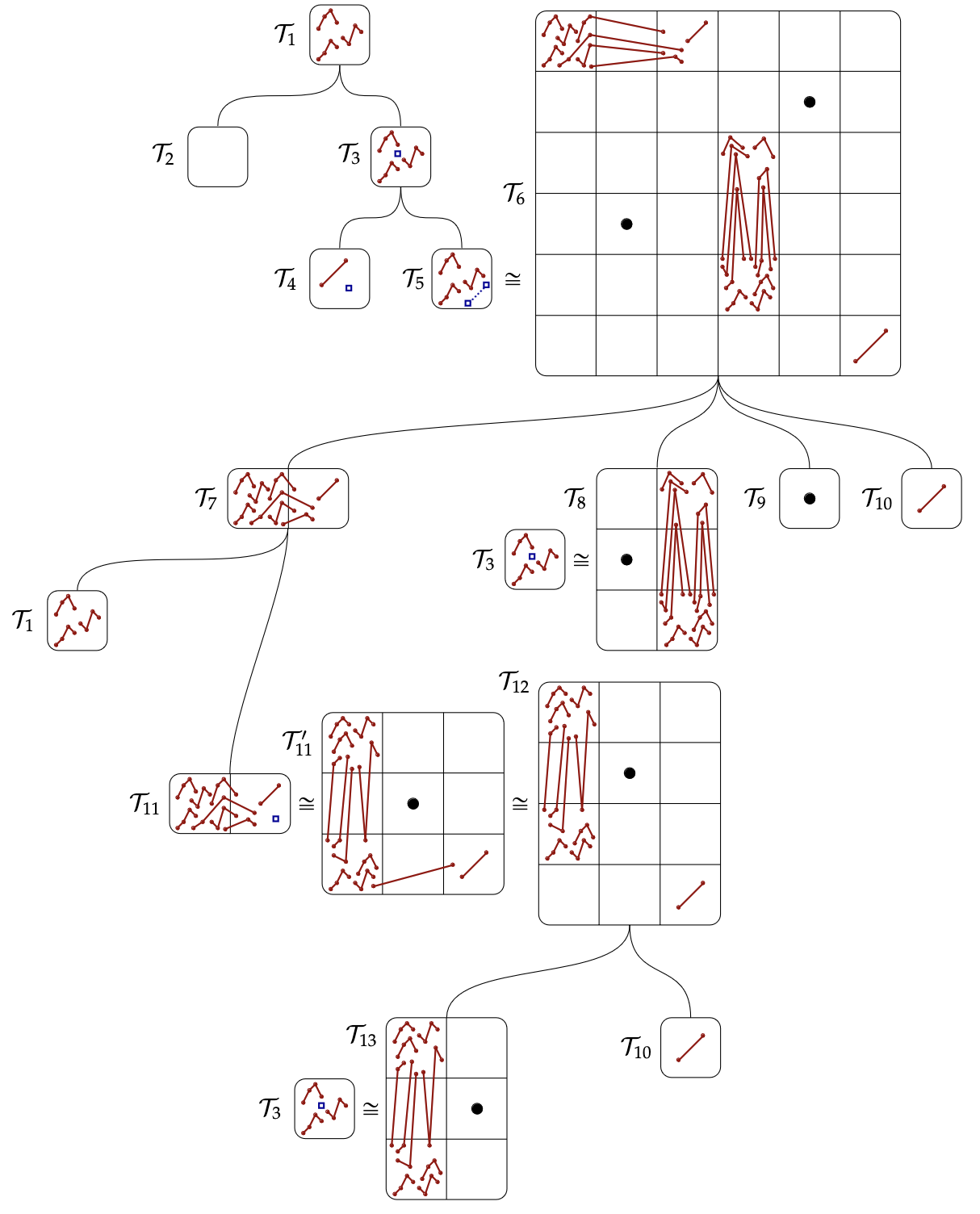
Combinatorial Exploration: An Algorithmic Framework for Enumeration
Under review. Available on arXiv.
Combinatorial Exploration is a new domain-agnostic algorithmic framework to automatically and rigorously study the structure of combinatorial objects and derive their counting sequences and generating functions. We describe how it works and provide an open-source Python implementation. As a prerequisite, we build up a new theoretical foundation for combinatorial decomposition strategies and combinatorial specifications. We then apply Combinatorial Exploration to the domain of permutation patterns, to great effect. We rederive hundreds of results in the literature in a uniform manner and prove many new ones. These results can be found in a new public database, the Permutation Pattern Avoidance Library (PermPAL) at https://permpal.com. Finally, we give three additional proofs-of-concept, showing examples of how Combinatorial Exploration can prove results in the domains of alternating sign matrices, polyominoes, and set partitions.
We enumerate permutations that avoid all but one of the \(k\) patterns of length \(k\) starting with a monotone increasing subsequence of length \(k-1\). We compare the size of such permutation classes to the size of the class of permutations avoiding the monotone increasing subsequence of length \(k-1\). In most cases, we determine the exponential growth rate of these permutation classes, while in the remanining cases, we present strong numerical evidence leading to a conjectured growth rate. We also present numerical evidence that suggests a conjecture for the growth rates of these permutation classes at subexponential precision. Some of these conjectures claim that the relevant permutation classes have non-algebraic, and in one case, even non-D-finite, generating functions.
Permutations that can be sorted greedily by one or more stacks having various constraints have been studied by a number of authors. A pop-stack is a greedy stack that must empty all entries whenever popped. Permutations in the image of the pop-stack operator are said to be pop-stacked. Asinowki, Banderier, Billey, Hackl and Linusson recently investigated these permutations and calculated their number up to length 16. We give a polynomial-time algorithm to count pop-stacked permutations up to a fixed length and we use it to compute the first 1000 terms of the corresponding counting sequence. With the 1000 terms we apply a pair of computational methods to prove some negative results concerning the nature of the generating function for pop-stacked permutations and to empirically predict the asymptotic behavior of the counting sequence using differential approximation.
Using Large Random Permutations to Partition Permutation Classes
Published in Pure Mathematics and Applications.
Permutation classes are sets of permutations defined by the absence of certain substructures. In some cases permutation classes can be decomposed as unions of subclasses. We use combinatorial specifications automatically discovered by Combinatorial Exploration: An algorithmic framework for enumeration, Albert et al. 2022, to uniformly generate large random permutations in a permutation class, and apply clustering methods to partition them into interesting subclasses. We seek to automate as much of this process as possible.

Worpitzky's identity, first presented in 1883, expresses \(n^p\) in terms of the Eulerian numbers and binomial coefficients: \[ n^p = \sum_{i=0}^{p-1}\genfrac<>{0pt}{}{p}{i}\binom{n+i}{p}. \] Pita-Ruiz recently defined numbers \(A_{a,b,r}(p,i)\) implicitly to satisfy a generalized Worpitzky identity \[ \binom{an+b}{r}^p = \sum_{i=0}^{rp} A_{a,b,r}(p,i) \binom{n+rp-i}{rp}, \] and asked whether there is a combinatorial interpretation of the numbers \(A_{a,b,r}(p,i)\). We provide such a combinatorial interpretation by defining a notion of descents in colored multipermutations, and then proving that \(A_{a,b,r}(p,i)\) is equal to the number of colored multipermutations of \(\{1^r, 2^r, \ldots, p^r\}\) with \(a\) colors and \(i\) weak descents. We use this to give combinatorial proofs of several identities involving \(A_{a,b,r}(p,i)\), including the aforementioned generalized Worpitzky identity.
A Structural Characterisation of \(\operatorname{Av}(1324)\) and New Bounds on its Growth Rate
Conference Paper — Published in Electronic Notes in Discrete Mathematics.
Full Paper — Published in European Journal of Combinatorics.
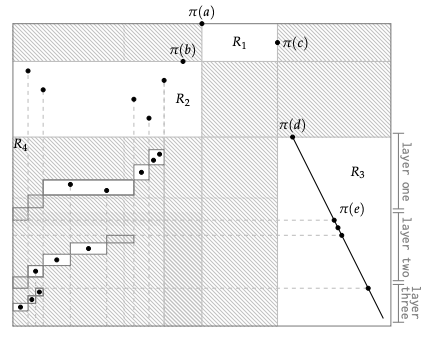
We establish an improved lower bound of 10.271 for the exponential growth rate of the class of permutations avoiding the pattern \(1324\), and an improved upper bound of 13.5. These results depend on a new exact structural characterisation of \(1324\)-avoiders as a subclass of an infinite staircase grid class, together with precise asymptotics of a small domino subclass whose enumeration we relate to West-two-stack-sortable permutations and planar maps. The bounds are established by carefully combining copies of the dominoes in particular ways consistent with the structural characterisation. The lower bound depends on concentration results concerning the substructure of a typical domino, the determination of exactly when dominoes can be combined in the fewest distinct ways, and technical analysis of the resulting generating function.
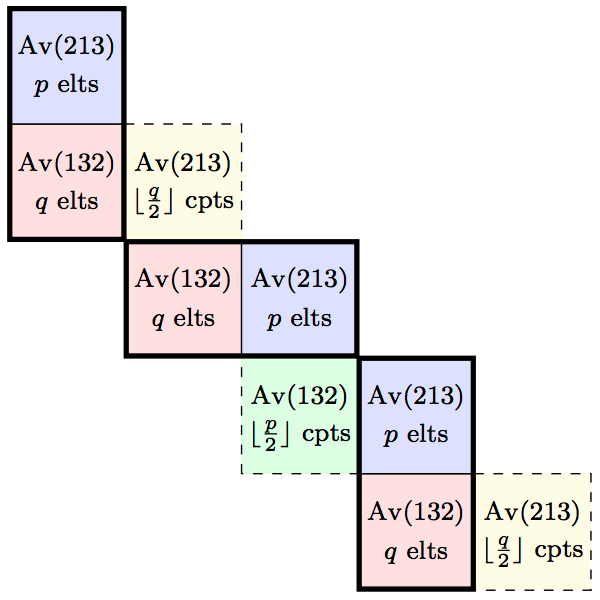
In the antecedent paper to this it was established that there is an algebraic number \(\xi\approx 2.30522\) such that while there are uncountably many growth rates of permutation classes arbitrarily close to \(\xi\), there are only countably many less than \(\xi\). Here we provide a complete characterization of the growth rates less than \(\xi\). In particular, this classification establishes that \(\xi\) is the least accumulation point from above of growth rates and that all growth rates less than or equal to \(\xi\) are achieved by finitely based classes. A significant part of this classification is achieved via a reconstruction result for sum indecomposable permutations. We conclude by refuting a suggestion of Klazar, showing that \(\xi\) is an accumulation point from above of growth rates of finitely based permutation classes.

There is a well-known upper bound on the growth rate of the merge of two permutation classes. Curiously, there is no known merge for which this bound is not achieved. Using staircases of permutation classes, we provide sufficient conditions for this upper bound to be achieved. In particular, our results apply to all merges of principal permutation classes. We end by demonstrating how our techniques can be used to reprove a result of Bóna.
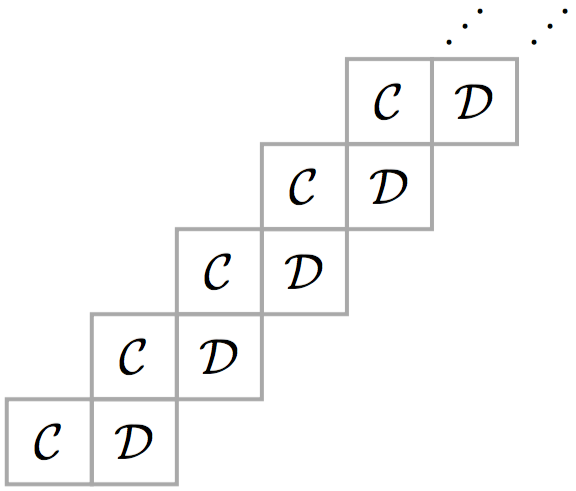
Universal Layered Permutations
Published in the Electronic Journal of Combinatorics.
We establish an exact formula for the length of the shortest permutation containing all layered permutations of length n, proving a conjecture of Gray.
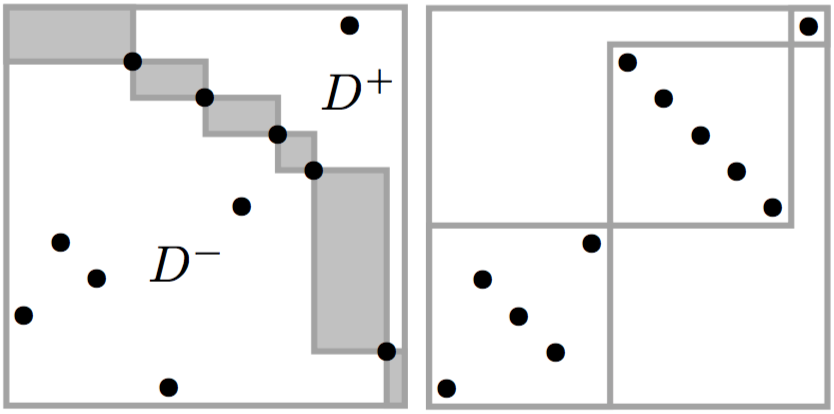
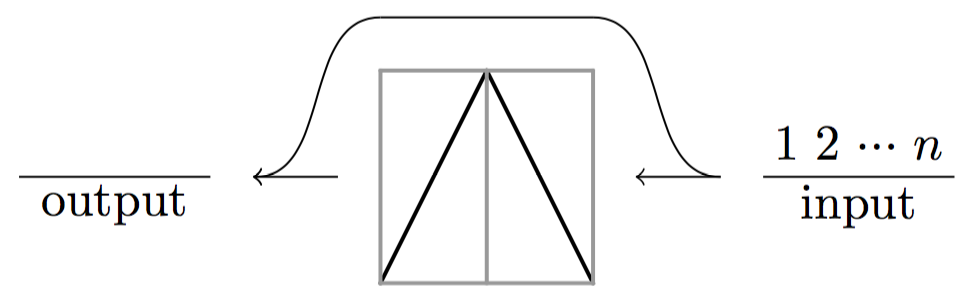
Generating Permutations with Restricted Containers
Published in the Journal of Combinatorial Theory, Series A.
We investigate a generalization of stacks that we call \(\mathcal{C}\)-machines. We show how this viewpoint rapidly leads to functional equations for the classes of permutations that \(\mathcal{C}\)-machines generate, and how these systems of functional equations can frequently be solved by either the kernel method or, much more easily, by guessing and checking. General results about the rationality, algebraicity, and the existence of Wilfian formulas for some classes generated by \(\mathcal{C}\)-machines are given. We also draw attention to some relatively small permutation classes which, although we can generate thousands of terms of their enumerations, seem to not have D-finite generating functions.
Completing the Structural Analysis of the 2x4 Permutation Classes
Available on arXiv.
We study the structure and enumeration of the final two 2x4 permutation classes, completing a research program that has spanned almost two decades. For both classes, careful structural analysis produces a complicated functional equation. One of these equations is solved with the guess-and-check paradigm, while the other is solved with kernel method-like techniques and Gröbner basis calculations.
Shift Equivalence in the Generalized Factor Order
Published in Archiv der Mathematik.
We provide a geometric condition that guarantees strong Wilf equivalence in the generalized factor order. This provides a powerful tool for proving specific and general Wilf equivalence results, and several such examples are given.
The Asymptotic Number of Simple Singular Vector Tuples of a Cubical Tensor
S. Ekhad and D. Zeilberger recently proved that the multivariate generating function for the number of simple singular vector tuples of a generic \(m_1 \times \cdots \times m_d\) tensor has an elegant rational form involving elementary symmetric functions, and provided a partial conjecture for the asymptotic behavior of the cubical case \(m_1 = \cdots = m_d\). We prove this conjecture and further identify completely the dominant asymptotic term, including the multiplicative constant. Finally, we use the method of differential approximants to conjecture that the subdominant connective constant effect observed by Ekhad and Zeilberger for a particular case in fact occurs more generally.

We find the generating function for the class of all permutations that avoid the patterns \(3124\) and \(4312\) by showing that it is an inflation of the union of two geometric grid classes.
Deflatability of Permutation Classes
Published in the Australasian Journal Combinatorics.
A permutation class is said to be deflatable if its simple permutations are contained within a proper subclass. Deflatable classes are often easier to describe, analyze, and enumerate than their non-deflatable counterparts. This paper presents theorems guaranteeing the non-deflatability of principal classes, constructs an infinite family of deflatable principal classes, and provides examples of each.
We study the class of non-holonomic power series with integer coefficients that reduce, modulo primes, or powers of primes, to algebraic functions. In particular we try to determine whether the susceptibility of the square-lattice Ising model belongs to this class, and more broadly whether the susceptibility is a solution of a differentially algebraic equation.
On Isomorphism Classes of Generalized Fibonacci Cubes
Published in the European Journal of Combinatorics.
The generalized Fibonacci cube \(Q_d(f)\) is the subgraph of the \(d\)-cube \(Q_d\) induced on the set of all strings of length \(d\) that do not contain \(f\) as a substring. It is proved that if \(Q_d(f) \cong Q_d(f')\) then \(|f|=|f'|\). The key tool to prove this result is a result of Guibas and Odlyzko about the autocorrelation polynomial associated to a binary string. It is also proved that there exist pairs of strings \(f, f'\) such that \(Q_d(f) \cong Q_d(f')\), where \(|f| \ge \frac{2}{3}(d+1)\) and \(f'\) cannot be obtained from \(f\) by its reversal or binary complementation. Strings \(f\) and \(f'\) with \(|f|=|f'|=d-1\) for which \(Q_d(f) \cong Q_d(f')\) are characterized.
Pattern Avoidance in Forests of Binary Shrubs
Published in Discrete Mathematics and Theoretical Computer Science.
We investigate pattern avoidance in permutations satisfying some additional restrictions. These are naturally considered in terms of avoiding patterns in linear extensions of certain forest-like partially ordered sets, which we call binary shrub forests. In this context, we enumerate forests avoiding patterns of length three. In four of the five non-equivalent cases, we present explicit enumerations by exhibiting bijections with certain lattice paths bounded above by the line \(y=\ell x\), for some \(\ell\in\mathbb{Q}^+\), one of these being the celebrated Duchon's club paths with \(\ell=2/3\). In the remaining case, we use the machinery of analytic combinatorics to determine the minimal polynomial of its generating function, and deduce its growth rate.
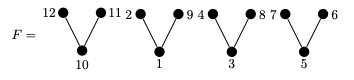
Pattern-Avoiding Involutions: Exact and Asymptotic Enumeration
Published in the Australasian Journal of Combinatorics.
We consider the enumeration of pattern-avoiding involutions, focusing in particular on sets defined by avoiding a single pattern of length 4. We directly enumerate the involutions avoiding \(1342\) and the involutions avoiding \(2341\). As we demonstrate, the numerical data for these problems exhibits some surprising behavior. This strange behavior even provides some very unexpected data related to the number of \(1324\)-avoiding permutations.
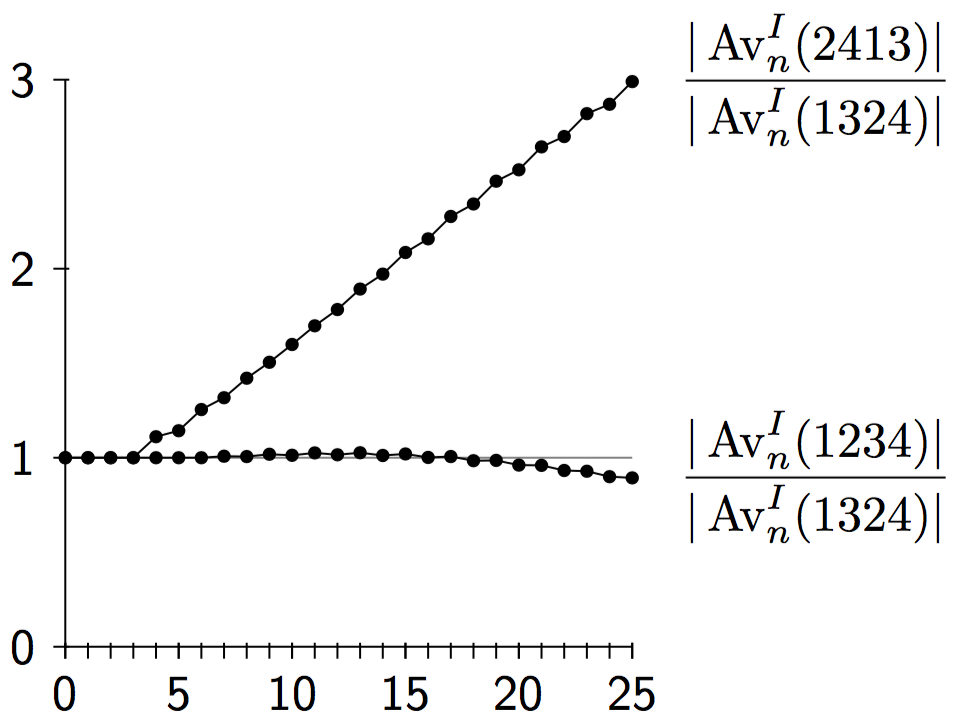
When two patterns occur equally often in a set of permutations, we say that these patterns are equipopular. Using both structural and analytic tools, we classify the equipopular patterns in the set of separable permutations. In particular, we show that the number of equipopularity classes for length \(n\) patterns in the separable permutations is equal to the number of partitions of the integer \(n-1\).
We prove that the set of patterns \(\{1324,3416725\}\) is Wilf-equivalent to the pattern \(1234\) and that the set of patterns \(\{2143,3142,246135\}\) is Wilf-equivalent to the set of patterns \(\{2413,3142\}\). These are the first known unbalanced Wilf-equivalences for classical patterns between finite sets of patterns.
The Rearrangement Conjecture states that if two words over \(\mathbb{P}\) are Wilf-equivalent in the factor order on \(\mathbb{P}^\ast\) then they are rearrangements of each other. We introduce the notion of strong Wilf-equivalence and prove that if two words over \(\mathbb{P}\) are strongly Wilf-equivalent then they are rearrangements of each other. We further conjecture that Wilf-equivalence implies strong Wilf-equivalence.